当前位置：文档视界 › 概率论

概率论

项目2 概率论、数据统计与区间估计

实验1 概率模型

实验目的通过将随机试验可视化, 直观地理解概率论中的一些基本概念, 从频率与概率的关系来体会概率的统计定义, 并初步体验随机模拟方法. 通过图形直观理解随机变量及其概率分布的特点.

基本命令

1.调用统计软包的命令

进行统计数据的处理, 必须调用相应的软件包, 首先要输入并执行命令

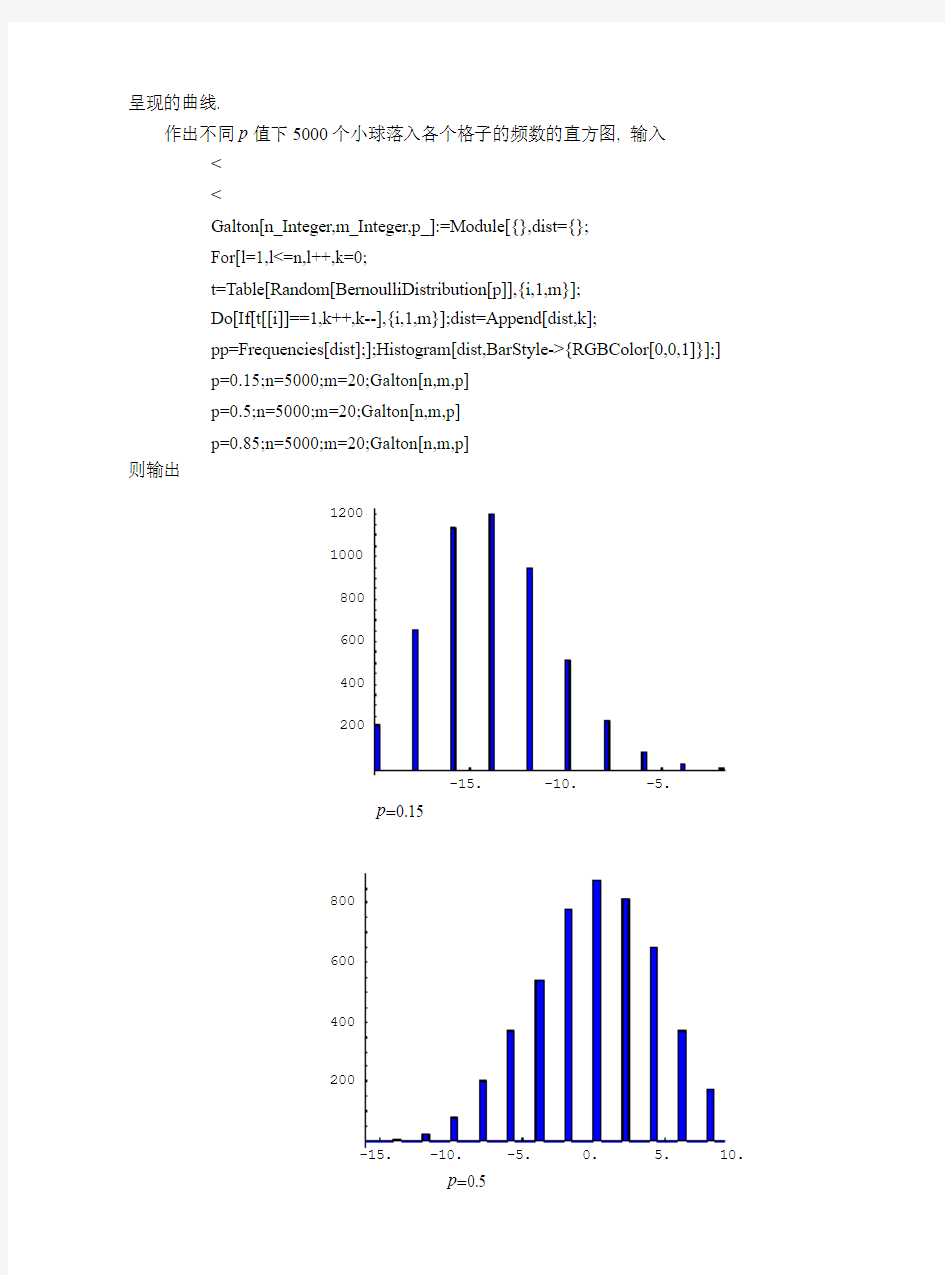
以完成数据统计的准备工作.

2.调用作图软件包的命令<

用Mathematica作直方图,必须调用相应的作图软件包,输入并执行

这时可以查询这个软件包中的一些作图命令的用法. 如输入

??BarChart

则得到命令BarChart的用法说明; 如果没有, 则说明调用软件包不成功, 必须重新启动计算机, 再次调用软件包.

实验举例

频率与概率

例1.1(高尔顿钉板实验)自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中, 当小球碰到钉子时从左边落下的概率为p, 从右边落下的概率为,

-碰到下一排钉子又

是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20

m排钉子, 下面进行模拟实验:

(1) 取,5.0

p自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观

察5次实验结果的共性及每次实验结果的偶然性;

(2) 分别取,

5000

n观察n个小球落下后p自板上端放入n个小球, 取,

.0,5.0,

呈现的曲线.

作出不同p值下5000个小球落入各个格子的频数的直方图, 输入<

Galton[n_Integer,m_Integer,p_]:=Module[{},dist={};

For[l=1,l<=n,l++,k=0;

t=Table[Random[BernoulliDistribution[p]],{i,1,m}];

Do[If[t[[i]]==1,k++,k--],{i,1,m}];dist=Append[dist,k];

pp=Frequencies[dist];];Histogram[dist,BarStyle->{RGBColor[0,0,1]}];]

p=0.15;n=5000;m=20;Galton[n,m,p]

p=0.5;n=5000;m=20;Galton[n,m,p]

p=0.85;n=5000;m=20;Galton[n,m,p]

则输出

p=0.15

p=0.5

p =0.85 图1-1

由图1-1可见: 若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0>p 曲线峰值的格子位置向右偏; 当,5.0

几何概型

例1.2 甲、乙二人约定八点到九点在某地会面, 先到者等20分钟离去, 试求两人能会面的概率.

由于甲、乙二人在[0,60]时间区间中任何时刻到达是等可能的, 若以X ,Y 分别代表甲乙二人到达的时刻, 则每次试验相当于在边长为60的正方形区域

}60,0);,{(≤≤=ΩY X Y X

中取一点.

设到达时刻互不影响, 因此),(Y X 在区域Ω内取点的可能性只与区域的面积大小成正比, 而与其形状、位置无关. 于是, 会面问题可化为向区域Ω随机投点的问题. 所关心的事件“二人能会面”可表示为

}20||);,{(≤-=Y X Y X A

(图1-2)

于是, 所求概率的理论值为

)(A P (A 的面积)/(Ω的面积)556.09

5≈=

图1-2

下面, 我们作如下模拟试验:

(1) 模拟向有界区域Ω投点n 次的随机试验, 取100=n , 统计每次投点是否落在图1-2 所示区域A 中, 若是则计数1次.

(2) 改变投点数,10000,5000,1000=n 统计落入区域A 的次数. 输入

meet[n_Integer]:=Module[{x},

x[k_]:=x[k]=Abs[Random[Integer,{0,60}]-Random[Integer,{0,60}]]; pile=Table[x[k],{k,1,n}];times=Count[pile,x_/;0<=x<=20]; Print[times];frequence=N[times/n]] n=100;meet[n] n=1000;meet[n] n=5000;meet[n] n=10000;meet[n]

则输出所求结果, 为方便比较, 将输出结果列于表1-1中

表1-1

从上表结果可见, 当约会次数越来越大时, 试验约会成功频率与理论约会成功概率越来越接近.

离散型随机变量及其概率分布

例1.3(二项分布)利用Mathematica 绘出二项分布),(p n b 的概率分布与分布函数的图形, 通过观察图形, 进一步理解二项分布的概率分布与分布函数的性质.

设20=n , ,2.0=p 输入

n=20;p=0.2;dist=BinomialDistribution[n,p];

t=Table[{PDF[dist,x+1],x},{x,0,20}];g1=BarChart[t,PlotRange->All]; g2=Plot[Evaluate[CDF[dist,x]],{x,0,20},PlotStyle->{Thickness[0.008],

RGBColor[0,0,1]}];

t=Table[{x,PDF[dist,x]},{x,0,20}];

gg1=ListPlot[t,PlotStyle->PointSize[0.03],DisplayFunction->Identity];

gg2=ListPlot[t,PlotJoined->True,DisplayFunction->Identity];

p1=Show[gg1,gg2,g1,DisplayFunction->$DisplayFunction,PlotRange->All];

则分别输出二项分布概率分布图形(图1-3)与分布函数图形(图1-4).

图1-3

图1-4

从图1-3可见, 概率}{k X P =随着k 的增加,先是随之增加, 直到4=k 达到最大值, 随后单调减少. 而从图1-4可见, 分布函数)(x F 的值实际上是x X ≤的累积概率值.

通过改变n 与p 的值, 读者可以利用上述程序观察二项分布的概率分布与分布函数随着n 与p 而变化的各种情况, 从而进一步加深对二项分布及其性质的理解.

连续型随机变量及其概率密度函数

例1.4 (正态分布)利用Mathematica 绘出正态分布),(2σμN 的概率密度曲线以及分布函数曲线, 通过观察图形, 进一步理解正态分布的概率分布与分布函数的性质.

(1) 固定,1=σ 取,2,0,2==-=μμμ 观察参数μ对图形的影响, 输入

dist=NormalDistribution[0,1]; dist1=NormalDistribution[-2,1]; dist2=NormalDistribution[2,1];

Plot[{PDF[dist1,x],PDF[dist2,x],PDF[dist,x]},{x,-6,6},

PlotStyle->{Thickness[0.008],RGBColor[0,0,1]},PlotRange->All];

Plot[{CDF[dist1,x],CDF[dist2,x],CDF[dist,x]},{x,-6,6},

PlotStyle->{Thickness[0.008],RGBColor[1,0,0]}];

则分别输出相应参数的正态分布的概率密度曲线(图1-5)及分布函数曲线(图1-6).

图1-6

从图1-5可见:

(a) 概率密度曲线是关于μ=x 对称的钟形曲线, 即呈现“两头小, 中间大, 左右对称” 的特点.

(b) 当μ=x 时, )(x f 取得最大值, )(x f 向左右伸展时, 越来越贴近x 轴.

(2) 固定0=μ, 取,5.1,1,5.0=σ观察参数σ对图形的影响, 输入

dist=NormalDistribution[0,0.5^2]; dist1=NormalDistribution[0,1]; dist2=NormalDistribution[0,1.5^2];

Plot[{PDF[dist1,x],PDF[dist2,x],PDF[dist,x]},{x,-6,6},

PlotStyle->{Thickness[0.008],RGBColor[0,0,1]},PlotRange->All]; Plot[{CDF[dist1,x],CDF[dist2,x],CDF[dist,x]},{x,-6,6},

PlotStyle->{Thickness[0.008],RGBColor[1,0,0]},PlotRange->All]; 则分别输出相应参数的正态分布的概率密度曲线(图1-7)及分布函数曲线(图1-8)

图1-7

从图1-7与图1-8可见: 固定μ, 改变σ时, σ越小, 在0附近的概率密度图形就变得越尖, 分布函数在0的附近增值越快; σ越大, 概率密度图形就越平坦, 分布函数在0附近的增值也越慢, 故σ决定了概率密度图形中峰的陡峭程度; 另外, 不管σ如何变化, 分布函数在 0点的值总是0.5, 这是因为概率密度图形关于0=x 对称.

通过改变μ与σ的值, 读者可以利用上述程序观察正态分布的概率分布与分布函数随着μ与σ而变化的各种情况, 从而进一步加深对正态分布及其性质的理解.

随机变量函数的分布

例1.5 设X ,Y 相互独立, 都服从(0,1)上的均匀分布, 求Y X Z +=的概率密度. 理论上, 我们可用卷积公式直接求出Y X Z +=的密度函数:

??≤≤-≤≤=其它,

021,210,

)(z z z z z g

下面, 我们作如下模拟试验:

(1) 产生两组服从(0,1)上均匀分布的相互独立的随机数,,,2,1,,n i y x i i = 取n ,1000= 计算;i i i y x z +=

(2) 用数据i z 作频率直方图, 并在同一坐标系内画出用卷积公式求得的密度函数图形作比较.

输入

Clear[g1,t,t1,t2];t={};n=1000;

g1[x_]:=50*Which[0<=x<=1,x,1<=x<=2,2-x,True,0];

pic1=Plot[g1[x],{x,0,2},PlotStyle->{Thickness[0.01],RGBColor[0,0,1]}]; t1=RandomArray[UniformDistribution[0,1],n]; t2=RandomArray[UniformDistribution[0,1],n]; Do[t=Append[t,t1[[i]]+t2[[i]]],{i,n}];p1=Histogram[t]; Show[pic1,p1,DisplayFunction->$DisplayFunction];

则在同一坐标系中输出所求频率直方图与密度函数的图形(图1-9).

中心极限定理的直观演示

例1.6 本例旨在直观演示中心极限定理的基本结论: “大量独立同分布随机变量的和的分布近似服从正态分布”. 按以下步骤设计程序:

(1) 产生服从二项分布),10(p b 的n 个随机数, 取2.0=p , 50=n , 计算n 个随机数之和y 以及

)

1(1010p np np y --;

(2) 将(1)重复1000=m 组, 并用这m 组)

1(1010p np np y --的数据作频率直方图进行观察.

输入

m=1000;n=50;p=0.2;t={};dist={}; For[i=1,i<=m,i++,

dist=RandomArray[BinomialDistribution[10,p],n]; ysum=CumulativeSums[dist];

nasum=(ysum[[n]]-10*n*p)/Sqrt[n*10*p*(1-p)];t=Append[t,nasum];] Histogram[t,FrequencyData->False];

则输出图1-10.

图1-10

从图1-10可见, 当原始分布是二项分布, n比较大时, n个独立同分布的的随机变量之和的分布近似于正态分布.

实验习题

1. (抛硬币实验) 模拟抛掷一枚均匀硬币的随机实验(可用0-1随机数来模拟实验结果), 取模拟n次掷硬币的随机实验. 记录实验结果, 观察样本空间的确定性及每次实验结果的偶然性, 统计正面出现的次数, 并计算正面出现的频率. 对不同的实验次数n进行实验, 记录下实验结果,通过比较实验的结果, 你能得出什么结论?

2. (抽签实验) 有十张外观相同的扑克牌, 其中有一张是大王, 让十人按顺序每人随机抽取一张, 讨论谁先抽出大王.

甲方认为: 先抽的人比后抽的人机会大.

乙方认为: 不论先后, 他们抽到大王的机会是一样的. 究竟他们谁说的对?

3. (泊松分布) 利用Mathematica在同一坐标系下绘出λ取不同值时泊松分布)

π的概

(λ

率分布曲线, 通过观察输出的图形, 进一步理解泊松分布的概率分布的性质.

4. (二项分布的正态分布逼近) 用正态分布逼近给出二项分布)

B,1

;

, 并将得到的近似值与它的精确值比较.

,2n

)

实验2 数据统计

实验目的掌握利用Mathematica求来自某个总体的一个样本的样本均值、中位数、样本方差、偏度、峰度、样本分位数和其它数字特征, 并能由样本作出直方图.

基本命令

1.求样本数字特征的命令

(1) 求样本list 均值的命令Mean[list]; (2) 求样本list 的中位数的命令Median[list]; (3) 求样本list 的最小值的命令Min[list]; (4) 求样本list 的最大值的命令Max[list]; (5) 求样本list 方差的命令V ariance [list];

(6) 求样本list 的标准差的命令StandardDeviation[list]; (7) 求样本list 的α分位数的命令Quantile[list,α]; (8) 求样本list 的n 阶中心矩的命令CentralMoment[list,n]. 2.求分组后各组内含有的数据个数的命令BinCounts 基本格式为

BinCounts [数据,{最小值,最大值,增量}]

例如,输入

BinCounts[{1,1,2,3,4,4,5,15,6,7,8,8,8,9,10,13},{0,15,3}]

则输出

{4,4,5,1,2}

它表示落入区间]15,12(],12,9(],9,6(],6,3(],3,0(的数据个数分别是4, 4, 5, 1, 2.

注: 每个区间是左开右闭的. 3.作条形图的命令BarChart 基本格式为

BarChart [数据,选项1,选项2,…]

其中数据是{{11,x y },{22,x y },…}或{ ,,21y y }的形式.而 ,,21y y 为条形的高度,

21,x x 为条形的中心.在数据为{ ,,21y y }的形式时默认条形的中心是{ ,2,1}.常用选项

有BarSpacing →数值1,BarGroupSpacing →数值2.

例如, 输入

BarChart[{{4,1.5},{4,4.5},{5,7.5},{1.10,5},{2,13.5}},BarGroupSpacing->0.1]

则输出如图2-1的条形图.

图2-1

实验举例

样本的数据统计

例2.1在某工厂生产的某种型号的圆轴中任取20个,测得其直径数据如下:

15.28,15.63,15.13,15.46,15.40,15.56,15.35,15.56,15.38,15.21,

15.48,15.58,15.57,15.36,15.48,15.46.15.52,15.29,15.42,15.69

求上述数据的样本均值,中位数,四分位数;样本方差,极差,变异系数,二阶、三阶和四阶中心矩;求偏度,峰度,并把数据中心化和标准化.

输入

data1={15.28,15.63,15.13,15.46,15.40,15.56,15.35,15.56,

15.38,15.21,15.48,15.58,15.57,15.36,15.48,15.46,

15.52,15.29,15.42,15.69}; (*数据集记为datal*)

Mean[data1] (*求样本均值*)

Median[data1] (*求样本中位数*)

Quartiles[data1] (*求样本的0.25分位数, 中位数, 0.75分位数*)

Quantile[data1,0.05] (*求样本的0.05分位数*)

Quantile[data1,0.95] (*求样本的0.95分位数*)

则输出

15.4405

15.46

{15.355,15.46,15.56}

15.13

15.63

即样本均值为15.4405,样本中位数为15.46,样本的0.25分位数为15.355,样本的0.75分位数 15.56, 样本的0.05分位数是15.13, 样本的0.95分位数是15.63.

输入

V ariance[data1] (*求样本方差2s *)

StandardDeviation[data1] (*求样本标准差s *) V arianceMLE[data1] (*求样本方差2*s *)

StandardDeviationMLE[data1] (*求样本标准差*s *) SampleRange[data1] (*求样本极差R *)

则输出

0.020605 0.143544 0.0195748 0.13991 0.56

即样本方差2s 为0.020605, 样本标准差s 为0.143544, 样本方差2*s 为0.0195748 样本标准差*s 为0.13991, 极差R 为0.56.

注: V ariance 给出的是无偏估计时的方差, 其计算公式为

∑=--n

i i

x x n 12

)

, 而 V arianceMLE 给出的是总体方差的极大似然估计, 其计算公式为∑=-n

i i

x x n

)

,它比前者稍

微小些.

输入

CoefficientOfV ariation[data1]

(*求变异系数.变异系数的定义是样本标准差与样本均值之比*)

则输出

0.00929662

输入

CentralMoment[data1,2](*求样本二阶中心矩*) CentralMoment[data1,3] (*求样本三阶中心矩*) CentralMoment[data1,4] (*求样本四阶中心矩*)

输出为

0.0195748 -0.00100041 0.000984863

输入

Skewness[data1]

(*求偏度,偏度的定义是三阶中心矩除以标准差的立方*)

Kurtosis[data1]

(*求峰度,峰度的定义是四阶中心矩除以方差的平方*)

则输出

-0.365287

2.5703

上述结果表明:数据(data1)的偏度(Skewness)是-0.365287,负的偏度表明总体分布密度有较长的右尾,即分布向左偏斜.数据(data1)的峰度(Kurtosis)为2.5703. 峰度大于3时表明总体的分布密度比有相同方差的正态分布的密度更尖锐和有更重的尾部. 峰度小于3时表明总体的分布密度比正态分布的密度更平坦或者有更粗的腰部.

输入

ZeroMean[data1]

(*把数据中心化,即每个数据减去均值*)

则输出

{-0.1605,0.1895,-0.3105,0.0195,-0.0405,0.1195,-0.0905,

0.1195,-0.0605,-0.2305,0.0395,0.1395,0.1295,-0.0805,

0.0395,0.0195,0.0795,-0.1505,-0.0205,0.2495}

输入

Standardize[data1](*把数据标准化,即每个数据减去均值,再除以标准差,从而使

新的数据的均值为0,方差为1*)

则输出

{-1.11812,1.32015,-2.16309,0.135846,-0.282143,0.832495,

-0.630467,0.832495,-0.421472,-1.60577,0.275176,

0.971825,0.90216,-0.560802,0.275176,0.135846,

0.553836,-1.04846,-0.142813,1.73814}

读者可验算上述新数据的均值为0,标准差为1.

作样本的直方图

例2.2从某厂生产的某种零件中随机抽取120个, 测得其质量(单位:g)如表2-1所示. 列出分组表, 并作频率直方图.

表2-1

200 202 203 208 216 206 222 213 209 219

216 203 197 208 206 209 206 208 202 203

206 213 218 207 208 202 194 203 213 211

193 213 208 208 204 206 204 206 208 209

213 203 206 207 196 201 208 207 213 208

210 208 211 211 214 220 211 203 216 221

211 209 218 214 219 211 208 221 211 218

218 190 219 211 208 199 214 207 207 214

206 217 214 201 212 213 211 212 216 206

210 216 204 221 208 209 214 214 199 204

211 201 216 211 209 208 209 202 211 207

220 205 206 216 213 206 206 207 200 198

输入

data2={200, 202, 203, 208, 216, 206, 222, 213, 209, 219,

216, 203, 197, 208, 206, 209, 206, 208, 202, 203,

206, 213, 218, 207, 208, 202, 194, 203, 213, 211,

193, 213, 208, 208, 204, 206, 204, 206, 208, 209,

213, 203, 206, 207, 196, 201, 208, 207, 213, 208,

210, 208, 211, 211, 214, 220, 211, 203, 216, 221,

211, 209, 218, 214, 219, 211, 208, 221, 211, 218,

218, 190, 219, 211, 208, 199, 214, 207, 207, 214,

206, 217, 214, 201, 212, 213, 211, 212, 216, 206,

210, 216, 204, 221, 208, 209, 214, 214, 199, 204,

211, 201, 216, 211, 209, 208, 209, 202, 211, 207,

220, 205, 206, 216, 213, 206, 206, 207, 200, 198};

先求数据的最小和最大值.输入

Min[data2]

Max[data2]

得到最小值190,最大值222.取区间[189.5,222.5],它能覆盖所有数据.将[189.5,222.5]等分为11

,这个小区间,设小区间的长度为3.0.数出落在每个小区内的数据个数,即频数)7,

(

,2,1

可以由BinCount命令来完成.

输入

f1=BinCounts[data2,{189.5,222.5,3}]

则输出

{1,2,3,7,14,20,23,22,14,8,6}

输入

gc=Table[189.5+j*3-1.5,{j,1,11}]

(*产生11个小区间的中心的集合gc*)

bc=Transpose[{f1/Length[data2],gc}]

(*Length[data2]为数据data2的总个数即样本的容量n, f1/Length[data2]为频率f i /n,Transpose 是求矩阵转置的命令, 这里bc 为数据对,第一个数是频率,第二个是组中心*)

则输出结果

.}}

221,201{.},218,15

.},215,60

7{.},212,60

11{

.},209,120

23{

.},

206,61{

.},203,60

.},200,1207{.},197,401{

.},194,60

.},191,120

1{{

输入作频率n f i /对组中心的条形图命令

BarChart[bc]

则输出所求条形图(图2-2).

图2-2

实验习题

1.在某省一“夫妻对电视传播媒介观念的研究”项目中,访问了30对夫妻,其中丈夫所受教育x (单位:年)的数据如下:

18,20,16,6,16,17,12,14,16,18,14,14,16,9,20,18,12,15,13,16,16,21,21,9,16,20,14,14,16,16 (1) 求样本均值、中位数、四分位数;样本方差、样本标准差、极差、变异系数,二阶、三阶和四阶中心矩;求偏度、峰度。

(2) 将数据分组,使组中值分别为6,9,12,15,18,21作出x 的频数分布表; 作出频率分布的直方图.

2.下面列出84个伊特拉斯坎男子头颅的最大宽度(单位:mm),对数据分组,并作直方图.

141 148 132 138 154 142 150 146 155 158

150 140 147 148 144 150 149 145 149 158

143 141 144 144 126 140 144 142 141 140

145 135 147 146 141 136 140 146 142 137

148 154 137 139 143 140 131 143 141 149

148 135 148 152 143 144 141 143 147 146

150 132 142 142 143 153 149 146 149 138

142 149 142 137 134 144 146 147 140 142

140 137 152 145

3.下面的数据是某大学某专业50名新生在数学素质测验中所得到的分数:

88,74,67,49,69,38,86,77,66,75,94,67,78,69,84,50,39,58,79,70,90,

79,97,75,98,77,64,69,82,71,65,68,84,73,58,78,75,89,91,62,72,74,

81,79,81,86,78,90,81,62

将这组数据分成6~8个组,画出频率直方图,并求出样本均值、样本方差,以及偏度、峰度.

实验3 区间估计

实验目的掌握利用Mathematica软件求一个正态总体的均值、方差的置信区间的方法; 求两个正态总体的均值差和方差比的置信区间的方法. 通过实验加深对统计推断的基本概

念的和基本思想的理解.

基本命令

1.调用区间估计软件包的命令<

用Mathematica作区间估计, 必须先调用相应的软件包. 要输入并执行命令

或

2.求单正态总体求均值的置信区间的命令MeanCi

命令的基本格式为

MeanCI[样本观察值, 选项1, 选项2,…]

其中选项1用于选定置信度, 形式为ConfidenceLevel->α

1, 缺省默认值为

ConfidenceLeve1->0.95. 选项2用于说明方差是已知还是未知,其形式为

knownV ariance->None或2

σ, 缺省默认值为knownV ariance->None. 也可以用说明标准差的

选项knownStandardDeviation->None或

σ来代替这个选项.

3. 求双正态总体求均值差的置信区间的命令MeanDifferenceCI

命令的基本格式为

MeanDifferenceCI[样本1的观察值, 样本2的观察值,选项1,选项2,选项3,…]

其中选项1用于选定置信度, 规定同2中的说明. 选项2用于说明两个总体的方差是已

知还是未知, 其形式为knownV ariance->2

0σ或},{2221σσ或None, 缺省默认值为

knownV ariance->None. 选项3用于说明两个总体的方差是否相等, 形式为

EqualVariance->False 或True. 缺省默认值为EqualV ariance->False, 即默认方差不相等.

4. 求单正态总体方差的置信区间的命令V arianceCI 命令的基本格式为

V arianceCI[样本观察值, 选项]

其中选项1用于选定置信度, 规定同2中的说明.

5. 求双正态总体方差比的置信区间的命令V arianceRatioCI 命令的基本格式为

V arianceRatioCI[样本1的观察值,样本2的观察值,选项]

其中选项1用于选定置信度, 规定同2中的说明. 6. 当数据为概括数据时求置信区间的命令

(1) 求正态总体方差已知时总体均值的置信区间的命令

NormalCI[样本均值, 样本均值的标准差, 置信度选项]

(2) 求正态总体方差未知时总体均值的置信区间的命令

StudentTCI[样本均值, 样本均值的标准差的估计, 自由度, 置信度选项] (3) 求总体方差的置信区间的命令

ChiSquareCI[样本方差, 自由度, 置信度选项]

(4) 求方差比的置信区间的命令

FRatioCI[方差比的值, 分子自由度, 分母自由度,置信度选项]

实验举例

单正态总体的均值的置信区间(方差已知情形)

例3.1 某车间生产滚珠, 从长期实践中知道, 滚珠直径可以认为服从正态分布. 从某天产品中任取6个测得直径如下(单位:mm):

15.6

16.3

15.9

15.8

16.2

16.1

若已知直径的方差是0.06, 试求总体均值μ的置信度为0.95的置信区间与置信度为0.90的

置信区间.

输入

MeanCI[data1,KnownV ariance->0.06] (*置信度采取缺省值*)

则输出

{15.7873,16.1793}

即均值μ的置信度为0.95的置信区间是(15.7063,16.2603).

为求出置信度为0.90的置信区间, 输入

MeanCI[data1,ConfidenceLevel->0.90,KnownV ariance->0.06]

则输出

{15.8188,16.1478}

即均值μ的置信度为0.90的置信区间是(15.7873,16.1793). 比较两个不同置信度所对应的置信区间可以看出置信度越大所作出的置信区间越大.

例3.2(教材§6.4 例1)某旅行社为调查当地旅游者的平均消费额, 随机访问了100名旅游者, 得知平均消费额80=x 元, 根据经验, 已知旅游者消费服从正态分布, 且标准差

12=σ元, 求该地旅游者平均消费额μ的置信度为%95的置信区间.

输入

NormalCI[80,12/25]

输出为

{77.648,82.352}

单正态总体的均值的置信区间(方差未知情形)

例3.3 (教材§6.4 例4)有一大批袋装糖果, 现从中随机地取出16袋, 称得重量(以克计) 如下:

506 508 499 503 504 510 497 512 514

505 493 496 506 502 509 496

设袋装糖果的重量近似地服从正态分布, 试求置信度分别为0.95与0.90的总体均值μ

的置信区间.

输入

data2={506,508,499,503,504,510,497,512,514,505,493,496,506,502,509,496}; MeanCI[data2]

(*因为置信度是0.95, 省略选项ConfidenceLeve1->0.95;

又方差未知, 选项knownV ariance->None 也可以省略*)

则输出

{500.445,507.055}

即μ的置信度为0.95的置信区间是(500.445,507.055).

再输入

MeanCI[data2,ConfidenceLevel->0.90]

则输出

{501.032,506.468}

即μ的置信度为0.90的置信区间是(501.032,506.468).

例3.4 从一批袋装食品中抽取16袋, 重量的平均值为,75.503g x =样本标准差为

.2022.6=s

假设袋装重量近似服从正态分布, 求总体均值μ的置信区间(05.0=α).

这里, 样本均值为503.75, 样本均值的标准差的估计为,4/2002.6/=n s 自由度为15, 05.0=α, 因此关于置信度的选项可省略.

输入

StudentTCI[503.75,6.2002/Sqrt[16],15]

则输出置信区间为

{500.446,507.054}

两个正态总体均值差的置信区间

例3.5(教材§6.4 例7)A , B 两个地区种植同一型号的小麦, 现抽取了19块面积相同的麦田, 其中9块属于地区A , 另外10块属于地区B , 测得它们的小麦产量(以kg 计) 分别如下:

地区A : 100 105 110 125 110 98 105 116 112 地区B : 101 100 105 115 111 107 106 121 102 92

设地区A 的小麦产量),(~211σμN X ,地区B 的小麦产量),(~222σμN Y ,2

21,,σμμ均未

知, 试求这两个地区小麦的平均产量之差21μμ-的95%和90%的置信区间. 输入

list1={100,105,110,125,110,98,105,116,112}; list2={101,100,105,115,111,107,106,121,102,92}; MeanDifferenceCI[list1,list2] (*默认定方差相等*)

则输出

{-5.00755,11.0075}

即21μμ-的置信度为95%的置信区间是(-5.00755, 11.0075).

输入

MeanDifferenceCI[list1,list2,EqualV ariances->True] (*假定方差相等*)

则输出

{-4.99382,10.9938}

这时21μμ-的置信度为0.95的置信区间是(-4.99382, 10.9938). 两种情况得到的结果基本一致.

输入

MeanDifferenceCI[list1,list2,ConfidenceLevel->0.90,EqualV ariances->True]

则输出

{-3.59115, 9.59115}

即21μμ-的置信度为90%的置信区间是(-3.59115, 9.59115). 这与教材结果是一致的.

例3.6 比较A 、B 两种灯泡的寿命, 从A 种取80只作为样本,计算出样本均值,2000=x 样本标准差.801=s 从B 种取100只作为样本, 计算出样本均值,1900=y 样本标准差.1002=s 假设灯泡寿命服从正态分布, 方差相同且相互独立, 求均值差21μμ-的置信区间

概率论与数理统计发展史

概率论与数理统计发展简史姓名：苗壮学号：1110810513 班级：1108105 指导教师：曹莉摘要：在这里，我们将简略地回顾一下概率论与数理统计的发展史，包括发展过程中所经历的一些大事，以及对这门学科的创立和发展有特别重大影响的那些学者的贡献．关键词：概率论、数理统计、发展史正文： 1.概率论的发展 17世纪，正当研究必然性事件的数理关系获得较大发展的时候，一个研究偶然事件数量关系的数学分支开始出现，这就是概率论．早在16世纪，赌博中的偶然现象就开始引起人们的注意．数学家卡丹诺(Cardano)首先觉察到，赌博输赢虽然是偶然的，但较大的赌博次数会呈现一定的规律性, 卡丹诺为此还写了一本《论赌博》的小册子，书中计算了掷两颗骰子或三颗骰子时，在一切可能的方法中有多少方法得到某一点数．据说，曾与卡丹诺在三次方程发明权上发生争论的塔尔塔里亚，也曾做过类似的实验．促使概率论产生的强大动力来自社会实践．首先是保险事业．文艺复兴后，随着航海事业的发展，意大利开始出现海上保险业务．16世纪末，在欧洲不少国家已把保险业务扩大到其它工商业上，保险的对象都是偶然性事件．为了保证保险公司赢利，又使参加保险的人愿意参加保险，就需要根据对大量偶然现象规律性的分析，去创立保险的一般理论．于是，一种专门适用于分析偶然现象的数学工具也就成为十分必要了．不过，作为数学科学之一的概率论，其基础并不是在上述实际问题的材料上形成的．因为这些问题的大量随机现象，常被许多错综复杂的因素所干扰，它使难以呈“自然的随机状态”．因此必须从简单的材料来研究随机现象的规律性，这种材料就是所谓的“随机博弈”．在近代概率论创立之前，人们正是通过对这种随机博弈现象的分析,注意到了它的一些特性, 比如“多次实验中的频率稳定性”等，然后经加工提炼而形成了概率论. 荷兰数学家、物理学家惠更斯（Huygens）于1657年发表了关于概率论的早期著作《论赌博中的计算》．在此期间，法国的费尔马（Fermat）与帕斯卡（Pascal）也在相互通信中探讨了随机博弈现象中所出现的概率论的基本定理和法则．惠更斯等人的工作建立了概率和数学期望等主要概念，找出了它们的基本性质和演算方法，从而塑造了概率论的雏形．18世纪是概率论的正式形成和发展时期．1713年，贝努利（Bernoulli）的名著《推想的艺术》发表．在这部著作中，贝努利明确指出了概率论最重要的定律之一――“大数定律”，并且给出了证明，这使以往建立在经验之上的频率稳定性推测理论化了，从此概率论从对特殊问题的求解，发展到了一般的理论概括．继贝努利之后，法国数学家棣谟佛（Abraham de Moiver）于1781年发表了《机遇原理》．书中提出了概率乘法法则，以及“正态分”和“正态分布律”的概念，为概率论的“中心极限定理”的建立奠定了基础． 1706年法国数学家蒲丰（Comte de Buffon）的《偶然性的算术试验》完成，他把概率和几何结合起来，开始了几何概率的研究，他提出的“蒲丰问题”就是采取概率的方法来求圆周率π的尝试．

概率论大作业讲解

现实生活中的大数定理及中心值定理的应用电子工程学院

目录摘要........................................... 错误！未定义书签。第一章引言...................................... 错误！未定义书签。第二章大数定律 (2) 2.1大数定律的发展历史 (2) 2.2大数定律的定义 (3) 2.3几个常用的大数定律 (3) 第三章大数定律的一些应用 (6) 3.1大数定律在数学分析中的一些应用 (6) 3.2大数定律在保险业的应用 (6) 3.3大数定律在银行经营管理中的应用 9结论 (11) 参考文献 (12)

对于随机现象而言,其统计规律性只有在基本相同的条件下进行大量的重复试验才能显现出来.本文主要是通过大数定律来讨论随机现象最根本的性质——平均结果稳定性的相关内容.大数定律,描述当试验次数很大时所呈现的概率性质的定律,是随机现象统计规律性的具体表现. 本文首先介绍了大数定律涉及的一些基础知识,以便于对文中相关知识的理解.通过比较,就不同条件下存在的大数定律做了具体的分析,介绍了几种较为常见的大数定律和强大数定律,总结了大数定律的应用,主要有大数定律在数学分析中的应用,大数定律在生产生活中的应用,大数定律在经济如：保险、银行经营管理中的应用等等,将理论具体化,将可行的结论用于具体的数学模型中,使大家对大数定律在实际生活中的应用价值有了更深的认识.

概率论与数理统计是研究随机现象的统计规律的科学,而随机现象的统计规律性只有在相同条件下进行大量重复试验或观察才呈现出来.在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律.大数定律是概率论中一个非常重要的课题,而且是概率论与数理统计之间一个承前启后的重要纽带.大数定律阐明了大量随机现象平均结果具有稳定性,证明了在大样本条件下,样本平均值可以看作总体平均值,它是“算数平均值法则”的基本理论,通俗地说,这个定理就是在试验不变的条件下,重复试验多次,随机事件的频率以概率为稳定值. 在现实生活中,经常可以见到这一类型的数学模型,比如,我们向上抛一枚硬币,硬币落下后哪一面朝上本来是偶然的,但当我们向上抛硬币的次数足够多时,达到上万次甚至几十万几百万次之后,我们会发现,硬币向上的次数约占总次数的二分之一,偶然中包含着必然.又如：在分析天平上称重量为a 的物品,若以12,,x x 3,...,n x x 表示n 次重复称量的结果,经验告诉我们,当n 充分大时,它们的算术平均值1 1n i i X n =∑与a 的偏差就越小.这种思想,不仅在整个概率论中起着重要00作用,而且在其他数学领域里面也占据着相当重要的地位. 大数定律的发展与研究也经历了很长一段时间,伯努利是第一个研究这一问题的数学家,他于1713年首先提出后人称之为“大数定律”的极限定理.现在,大数定律的相关模型已经被国内外广大学者所研究,特别是应用在实际生活中,如保险业得以存在并不断发展壮大的两大基石的一个就是大数定律.许多学者也已经在此领域中研究出了许多有价值的成果,讨论了在统计,信息论,分析、数论等方面的应用.在许多数学领域中,广大学者对某些具有特定类型的数学模型,都能利用大数定律的思考方式总结其代表性的性质及结论,使得这些类型的数学模型在进行讨论的时候大大简化了繁琐的论证过程,方便了研究.大数定律作为概率论的重要内容,其理论成果相对比较完善,这方面的文章较多,结果也比较完美,但对大数定律的应用问题的推广也是一项非常有价值的研究方向,通过对这些问题的应用推广,不仅能加深对大数定律的理解,而且能使之更为有效的服务于各项知识领域中.下面文中就通过对大数定律的讨论,给出了各大数定律之间的关系,归结出一般性结论.最后列举了一些能用大数定律来解决的实例,希望能通过这些实例,来进一步阐明大数定律在各个分支学科中的重要作用,以及在实际生活中的应用价值,加深大家对大数定律的理解.

概率计算方法全攻略

概率计算方法全攻略在新课标实施以来，中考数学试题中加大了统计与概率部分的考查，体现了“学以致用”这一理念. 计算简单事件发生的概率是重点，现对概率计算方法阐述如下: 一.公式法 P(随机事件)= 的结果数随机事件所有可能出现果数随机事件可能出现的结.其中P(必然事件)=1,P （不可能事件） =0；0

概率论论文

概率论与数理统计总结（1-5章节）第一章&第二章概率论引论& 条件概率本章知识点： 1．随机事件及其运算（随机试验，随机事件与样本空间，事件之间的关系及其运算） 2．概率的定义、性质及其运算（频率，概率的统计定义，古典概率，概率的公理化定义，概率的性质） 3．条件概率及三个重要公式（乘法公式，全概率公式，贝叶斯公式） 4．事件的独立性及贝努里(Bernoulli)概型理解重点： 1.理解随机事件的概念，了解样本空间的概念，掌握事件的关系与基本运算； 2.理解事件频率的概念，了解随机现象的统计规律性，理解概率的公理化定义和概率的其它性质； 3.理解古典概率的定义，掌握古典概率的计算，了解几何概率的定义及计算； 4.掌握概率的基本性质和应用这些性质进行概率计算； 5.理解条件概率的概念，熟练掌握条件概率的计算，熟练掌握乘法公式、全概率公式和贝叶斯公式以及应用这些公式进行概率计算； 6.理解事件的独立性概念，掌握应用事件独立性进行概率计算，理

解贝努利试验的概念，熟练掌握二项概率公式（贝努利概型）及其应用。第一节随机事件一、概率论序言二、随机试验与随机事件（一）随机试验 1．试验可在相同条件下重复进行； 2．每次试验的可能结果不止一个，而究竟会出现哪一个结果，在试验前不能准确地预言； 3．试验所有可能结果在试验前是明确(已知)的，而每次试验必有其中的一个结果出现，并且也仅有一个结果出现。满足上述三个特性的试验，叫做随机试验，简称试验，并用字母E 等表示。（二）随机事件随机试验的结果称为随机事件，简称事件。 1．必然事件：在试验中一定出现的结果，记作Ω； 2．不可能事件：在试验中一定不会出现的结果，记作Φ； 3．随机事件：在试验中可能出现也可能不出现的结果，常用大写拉丁字母A、B、C…表示； 4．基本事件(样本点)：试验最基本的结果，记作ω； 5．样本空间(基本事件空间)：所有基本事件的集合，常用Ω表示；样本空间Ω中的元素是随机试验的可能结果。样本空间的任一子集称

概率论习题及答案()

概率论习题一、填空题 1、掷21n +次硬币，则出现正面次数多于反面次数的概率是 . 2、把10本书任意的放到书架上，求其中指定的三本书放在一起的概率. 3、一批产品分一、二、三级，其中一级品是二级品的两倍，三级品是二级品的一半，从这批产品中随机的抽取一件，试求取到二级品的概率 . 4、已知()0.7,()0.3,P A P A B =-= 则().P AB = 5、已知()0.3,()0.4,()0.5,P A P B P AB === 则(|).P B A B ?= 6、掷两枚硬币，至少出现一个正面的概率为.. 7、设()0.4,()0.7,P A P A B =?= 若,A B 独立，则().P B = 8、设,A B 为两事件，11()(),(|),36 P A P B P A B === 则(|).P A B = 9、设123,,A A A 相互独立，且2(),1,2,3,3i P A i == 则123,,A A A 最多出现一个的概率是. 10、某人射击三次，其命中率为0.8，则三次中至多命中一次的概率为 . 11、一枚硬币独立的投3次，记事件A =“第一次掷出正面”，事件B =“第二次掷出反面”，事件C =“正面最多掷出一次”。那么(|)P C AB = 。 12、已知男人中有5%是色盲患者，女人中有0.25%是色盲患者.今从男女人数相等的人群中随机地表示为互不相容事件的和是。15、,,A B C 中不多于两个发生可表示为。二、选择题 1、下面四个结论成立的是（） 2、设()0,P AB =则下列说法正确的是（） 3、掷21n +次硬币，正面次数多于反面次数的概率为（） 4、设,A B 为随机事件，()0,(|)1,P B P A B >= 则必有（） 5、设A 、B 相互独立，且P (A )>0，P (B )>0，则下列等式成立的是（） .A P (AB )=0 .B P (A -B )=P (A )P (B ) .C P (A )+P (B )=1 .D P (A |B )=0 6、设事件A 与B 互不相容，且P (A )>0，P (B ) >0，则有（） .A P (AB )=l .B P (A )=1-P (B ) .C P (AB )=P (A )P (B ) .D P (A ∪B )=1

概率统计论浅谈泊松分布

浅谈泊松分布班级：XXX 姓名：XXX 学号：XXX

浅谈泊松分布当一个随机事件，以固定的平均瞬时速率λ

二项概率的泊松逼近如果∞→n ，0→p 使得λ=np 保持为正常数，则 λλ--→-e k p p C k k n k k n !)1( 对k = 0,1,2,…一致地成立。

2.1泊松分布使用范围泊松分布主要用于描述在单位时间(空间)中稀有事件的发生数. 即需满足以下四个条件： 1. 给定区域内的特定事件产生的次数，可以是根据时间，长度，面积来定义； 2. 各段相等区域内的特定事件产生的概率是一样的； 3. 各区域内，事件发生的概率是相互独立的；

4. 当给定区域变得非常小时，两次以上事件发生的概率趋向于0。 2.2泊松分布的性质 1. 泊松分布的均数与方差相等，即m =2σ 2．泊松分布的可加性如果1x ，2x ，3x …k x 相互独立，且它们分别服从以1λ，2λ，3λ…k λ为参数的泊松分布，则k X X X X T ++++= 321也服从泊松分布，其参数为k λλλλ++++ 321。 3.泊松分布的应用 )0(P 是未产生二体的菌的存在概率，实际上其值的5%与采用2/05.0m J 照射时的大肠杆菌uvrA -株，recA -株（除去既不能修复又不能重组修复的二重突变）的生存率是一致的。由于该菌株每个基因

组有一个二体就是致死量，因此)1(P ，)2(P ……就意味着全部死亡的概率。 3.2泊松分布在医学统计上的应用在遗传学上，计算遗传图距的基本方法是建立在重组率基础上的，根据重组率的大小作出有关基因间的距离，绘制线性基因图；可是当研究的两个基因间的距离相对较远，在它们之间可能发生双交换、三交换、四交换甚至更高数目的交换，而形成的配子总有一半是非重组型的。若简单的把重组率看作交换率，显然交换率降低了，图距也随之缩小。这里可以用泊松分布原理来描述减数分裂过程中染色体上某区段交换的分布。在图距计算中，x 表示交换数，m 表示对总样本来说每进行一次减数分裂两基因间的平均交换数，而基因间不发生交换的概率为m m e e m P --==! 0)0(0 ，基因间至少发生一次交换的概率为m e P P --=-=1)0(1。由此可计算两基因间的交换率和重组率。进而可更科学的作出遗传图。 3.3 泊松分布在交通运输上的应用道路是行驶各种车辆的通道。为了给编制交通建设规划提供可靠的依据和保证道路上的车能安全而有效地通行, 道路工作者必须对道路上的车流进行实地调查和统计分析以便掌握车流的变化规律。数理统计方法是对交通流分布进行研究的有效而实际可行的方法。通常把在单位时间内通过道路上某一地点的车辆叫做交通流。对于时间间隔极短,并非是高密度的交通流的分布状态, 它常常是服从“概率论” 中的“ 泊松分布” 规律的。如用简单例子表示，取通过某一地点车辆的时间作为时间数轴, 在数轴上划出给定时间间隔和该时间间隔内通过的车辆数目,譬如, 以20秒的时间间隔的数轴为例, 在20~0秒内,一辆车也没有通过, 在40~20秒间隔内,有二辆车通过, 在60~40秒间隔内, 有一辆车通过, 等等。这样在实地进行大量观测就可以的到某一时间间隔内的随机来车数目和该时间间隔内出现该车辆数的次数, 从而按泊松分布公式求算在给定时间间隔内在某一地点通过γ辆车的概率)(γP 。参考文献 1．戴维 M. 莱文等.《以EXCEL 为决策工具的商务统计》.机械工业出版社，2009 2．庄军、林奇英《泊松分布在生物学中的应用》.激光生物学报.2007年第16卷第5期. 3．薛珊荣《“泊松分布”在交通工程中的应用》.湖南大学学报.1995年第8卷第2期.

概率论与数理统计公式整理超全免费版

第1章随机事件及其概率（1）排列组合公式 )! ( ! n m m P n m- =从m个人中挑出n个人进行排列的可能数。 )! (! ! n m n m C n m- =从m个人中挑出n个人进行组合的可能数。（2）加法和乘法原理加法原理（两种方法均能完成此事）：m+n 某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由n种方法来完成，则这件事可由m+n 种方法来完成。乘法原理（两个步骤分别不能完成这件事）：m×n 某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n 种方法来完成，则这件事可由m×n 种方法来完成。（3）一些常见排列重复排列和非重复排列（有序）对立事件（至少有一个）顺序问题（4）随机试验和随机事件如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。试验的可能结果称为随机事件。（5）基本事件、样本空间和事件在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质： ①每进行一次试验，必须发生且只能发生这一组中的一个事件； ②任何事件，都是由这一组中的部分事件组成的。这样一组事件中的每一个事件称为基本事件，用ω来表示。基本事件的全体，称为试验的样本空间，用Ω表示。一个事件就是由Ω中的部分点（基本事件ω）组成的集合。通常用大写字母A，B，C，…表示事件，它们是Ω的子集。 Ω为必然事件，?为不可能事件。不可能事件（?）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω）的概率为1，而概率为1的事件也不一定是必然事件。（6）事件的关系与运算①关系：如果事件A的组成部分也是事件B的组成部分，（A发生必有事件B发生）：B A? 如果同时有B A?，A B?，则称事件A与事件B等价，或称A等于B：A=B。 A、B中至少有一个发生的事件：A B，或者A+B。属于A而不属于B的部分所构成的事件，称为A与B的差，记为A-B，也可表示为A-AB或者B A，它表示A发生而B不发生的事件。 A、B同时发生：A B，或者AB。A B=?，则表示A与B不可能同时发生，称事件A与事件B互不相容或者互斥。基本事件是互不相容的。 Ω-A称为事件A的逆事件，或称A的对立事件，记为A。它表示A不发生的

概率论论文

概率论论文【摘要】概率论是研究随机现象规律性的一个数学分支，它来源于实际生活，也解决了实际生活中的许多问题。小概率事件是概率论中的一个具有实用意义的原理，在我们的日常生活中已经有广泛的应用。本文重点讨论的内容有：小概率事件的含义、小概率原理以及用彩票阐述小概率事件在日常生活中的实际应用，给出几点彩票玩法建议，并使人们对生活中的小概率事件树立正确的认识。【Abstract】Probability theory is a mathematics branch of random phenomena regularity study, it comes from the actual life, and also solves many problems in actual life. Probability of small probability events is a principle of practical significance in our daily life which has a wide application. What is mainly discussed in this paper is the meaning of small probability events, small probability principle and the actual application expounded by lottery，small probability events in daily life, and suggestions about lottery play helping people establish correct understanding of small probability events. 【关键词】小概率事件彩票二项分布泊松分布【Keywords】Small probability events,Lottery, Binomial distribution, Poisson distribution 1 引言随着彩票在全国乃至全球的火热发行，对有些人来说，博彩已成为生活的一部分，影响之大不言而喻。由“一夜暴富”心理导致的盲目购买彩票已经成了社会的一个大问题，因此，虽然现在买彩票的人越来越多，但其中真正理智买彩票的却不多。大家都想把彩票当钞票，要知道即开彩大奖是属于小概率事件。社会上各种彩票的方式，玩法不尽相同，但是万变不离其宗，都包含了共同的规律。在这样的背景下我研究“小概率事件在彩票中的应用”是大有意义的。概率学是专门研究随机事件规律的科学，它在彩票的购买中起着重要的作用，是概率论中一个简单但又极其有用的原理，是统计学存在、发展的基础。小概率事件作为在统计推断的理论及应用中有着重要作用的一个基本原理——实际推断原理，即小概率事件在一次试验中实际上是几乎不发生的，我们可以把它看成是不可能事件，这是概率论应用中的一条最基本的原理。对于自然界中的

概率论

一 1、若事件A 出现，事件B 和事件C 都不出现，则可表示为。 2、已知,6.0)(,4.0)(,==?B P A P B A 则)(A B P -= 。 3、皮尔逊做掷一枚均匀硬币的试验，观察“正面朝上”这一事件A ，在12000次试验中，事件A 出现了6019次，则事件A 出现的频率是。 4、已知随机变量A 的概率,5.0)(=A P 随机事件B 的概率,6.0)(=B P 条件概率 ,8.0)|(=A B P 则=?)(B A P 。 5、某工厂有甲、乙、丙三个车间生产同一种产品，每个车间的产量分别占全厂的%,40%,35%,25各个车间产品的次品率分别为%,2%,4%,5则该厂产品的次品率为。 6、假设X 是连续型随机变量，其概率密度函数为???<<=. 030)(2其它，；，x cx x f ，则 =c 。 7、设二维随机变量 ) ,(Y X 的联合分布函数为 ),arctan )(arctan (),(y C x B A y x F ++=则=A ，=B ，=C 。 8、设Y 服从)4,5.1(N ，则=>}2{X P 。 9、设随机变量)16,1(~),4,1(~N Y N X ，则=+)(Y X E 。 10、设X 和Y 是相互独立，X 服从标准正态分布，Y 服从自由度为n 的卡方分布，称随机变量：n Y X T = 的分布为自由度为的分布。二、设有一批量为50的同型号产品，其中次品10件，现按以下两种方式随机抽取2件产品：（1）有放回抽取，即先任取一件，观察后放回批中，再从中任取一件；（2）不放回抽取，即先任取一件，观察后不放回批中，从剩余的产品中再任取一件。试分别按这两种抽取方式，求 (a)、两件都是次品的概率？ (b)、第一件是次品，第二件是正品的概率？

浅谈初中教材中的概率与统计

浅谈初中教材中的概率与统计发表时间：2015-06-12T14:46:19.687Z 来源：《中小学教育》2015年5月总第206期供稿作者：张永辉 [导读] 但是目前人教版初中数学教材却把这部分内容作为选学教材，导致教学中出现了诸多误区。张永辉淮北师范大学数学科学学院235000 摘要：大数据时代，概率统计与我们的生活关系越来越密切。但是目前人教版初中数学教材却把这部分内容作为选学教材，导致教学中出现了诸多误区。笔者认为须将初中数学“概率与统计”的教学内容做进一步研究、澄清，以提高师生认识，达到学习为生活储备、教学为社会服务的目的。关键词：概率与统计数据误区一、教学现状及教材内容分析新课标提出：义务教育阶段的学生应该了解概率与统计的基本思想方法，逐步形成统计观念。中学生在小学中已接触过少量有关统计方面的知识与方法，如计算平均值、了解一些可能性的事件；初步的调查，如“同学们喜欢哪项运动”，绘制条形统计图等。这些内容架起了与初中数学概率与统计内容之间的桥梁。初中阶段的概率与统计分三学段进行：第一学段，体验数据统计的过程，掌握一些简单数据的收集、整理和描述的方法，感受事件发生的可能性；第二学段，经历简单数据统计过程，会根据数据分析的结果做出判断与预测，能计算一些简单事件发生的可能性；第三学段，从事数据的收集、整理与描述的过程，体会抽样的必要性，以及用样本估计总体的思想，进一步体会概率的意义，能计算简单事件发生的概率。二、教师和学生对其认识上的误区在人教版初中教材传统的概率与统计教学中，数据分析、概率、频率这部分内容都没有安排，只安排了概率的基础知识、平均值、方差、排列与组合等与精确数学接近的相关内容。在新课改的教材中，这种状况虽然得到了改善，但相当一部分学生对概率与统计学还存在一定的认识障碍。 1.教师思想不够重视。概率与统计部分与其他代数或几何内容不同，教学时需要让学生参与计算、分析与判断。还有教材安排上三个年级分段教学，每次只有一小部分内容，这样大部分教师就忽视了其重要性，认为是选学内容，一带而过，没有真正理解教材按照学生的认知规律安排教材的意图。事实上对统计与概率的接受需要经历收集数据、检验并调整自己的直觉等过程，这需要延续较长的时间，才能形成较为完整的概率统计意识。 2.学生理解存在偏差。初中生已经历过前运算阶段（七八岁）与具体运算阶段（七八岁到十二岁左右），差不多开始进入形式运算阶段，但演绎逻辑与随机概念还比较缺乏，比如主观判断、预言结果、用自己的方法统计与计算、因果事件与随机事件的区分等等，总认为没有发生的总比发生过的更容易出现。例如，总共投1000次硬币，已投了999次都是正面朝上，那么，他认为在投第1000次时一定会出现反面朝上。有的学生在学习数据处理时不能区分有效与无效数据，抓不住重点数据，不能做出合理归纳与引用。三、改进措施针对上述师生在概率与统计教学过程中的错误认识和偏颇理解，我们应该从以下三方面进行改进： 1.通过活动组织概率与统计的教学。教师应通过课堂实践活动来改变学生存在的一些偏颇理解和错误认识。在活动过程中，教师要改变常规的讲授教学法，采用实践教学活动来引领学生学习，教师作为活动的组织者与合作者，让学生通过交流合作、主动探究，在收集和处理数据的实践中去领悟。如在概念讲解中要多举例子，让抽象的概念和生活实际联系起来，这样便于学生理解。同时，教师还要着意培养学生正确的学习方法，提倡合作、探究、实践、创新的学习精神，充分体现学生在学习中的主体地位。 2.借助练习加深学生理解。概率与统计的教学仅用口头教授的方法很难改变学生直觉，即使教师多次讲解、反复强调，但学生还是可能出现理解偏差。教师应创设情境，引导学生用真实的数据、活动以及直观的模拟实验让学生由浅入深、由具象到抽象地认识；有可能的话，还可以让学生走出课堂，通过深入调查生活中的事例，综合考虑多方面的因素做出合理估计与统计，进而化纯知识为能力。例如，概率初步中有这样一道题：同时投掷两个质地均匀的骰子，计算下列事件的概率：（1）两个骰子的点数相同；（2）两个骰子点数和是9；（3）至少有一个骰子的点数是2。我们都知道每个骰子出现的点数无非就是“1、2、3、4、5、6”，那么每次投掷两个质地均匀的骰子出现的点数组合的排列，我们很快就能列举出来，自然会得出正确答案，这就要学生亲自动手操作。类似的，同时投掷两枚硬币，问正面向上的概率、一正一反的概率是多少，也可以用这种数字模型去做。 3.充分发挥现代化教学媒体的作用。现代的多媒体课件具有文字、图片、声音、动画等直观的效果，这种动态演示能强有力地吸引学生，激发学生的求知欲。在概率计算中，往往数据复杂，可以允许学生用计算器来处理繁杂的计算，容易调动学生的学习兴趣。同时可以将学习重点放在理解统计思想和从事统计活动上来，避免将这些内容变成单纯的数学计算。要想在教学过程中教好概率统计，首先，需要教师先学好概率统计的相关知识，深刻了解它在教材中的作用和地位；其次，结合学生的实际学情，遵循学生的接受能力、认识水平，处理好教材与生活的联系，方能事半功倍。

概率论与数理统计知识点总结(免费超详细版)

《概率论与数理统计》第一章概率论的基本概念 §2．样本空间、随机事件 1．事件间的关系 B A ?则称事件B 包含事件A ，指事件A 发生必然导致事件B 发生 B }x x x { ∈∈=?或A B A 称为事件A 与事件B 的和事件，指当且仅当A ，B 中至少有一个发生时，事件B A ?发生 B }x x x { ∈∈=?且A B A 称为事件A 与事件B 的积事件，指当A ，B 同时发生时，事件B A ?发生 B }x x x { ?∈=且—A B A 称为事件A 与事件B 的差事件，指当且仅当A 发生、B 不发生时，事件B A —发生 φ=?B A ，则称事件A 与B 是互不相容的，或互斥的，指事件A 与事件B 不能同时发生，基本事件是两两互不相容的且S =?B A φ=?B A ，则称事件A 与事件B 互为逆事件，又称事件A 与事件B 互为对立事件 2．运算规则交换律A B B A A B B A ?=??=? 结合律)()( )()(C B A C B A C B A C B A ?=???=??

分配律 )()B (C A A C B A ???=??）（ ))(()( C A B A C B A ??=?? 徳摩根律B A B A A B A ?=??=? B — §3．频率与概率定义在相同的条件下，进行了n 次试验，在这n 次试验中，事件A 发生的次数A n 称为事件A 发生的频数，比值n n A 称为事件A 发生的频率概率：设E 是随机试验，S 是它的样本空间，对于E 的每一事件A 赋予一个实数，记为P （A ），称为事件的概率 1．概率)(A P 满足下列条件：（1）非负性：对于每一个事件A 1)(0≤≤A P （2）规范性：对于必然事件S 1)S (=P （3）可列可加性：设n A A A ,,,21Λ是两两互不相容的事件，有∑===n k k n k k A P A P 1 1 )()(Y （n 可以取∞） 2．概率的一些重要性质：（i ） 0)(=φP （ii ）若n A A A ,,,21Λ是两两互不相容的事件，则有∑===n k k n k k A P A P 1 1 )()( Y （n 可以取∞）

概率论毕业论文外文翻译

Statistical hypothesis testing Adriana Albu，Loredana Ungureanu Politehnica University Timisoara,adrianaa@aut.utt.ro Politehnica University Timisoara,loredanau@aut.utt.ro Abstract In this article,we present a Bayesian statistical hypothesis testing inspection, testing theory and the process Mentioned hypothesis testing in the real world and the importance of, and successful test of the Notes. Key words Bayesian hypothesis testing; Bayesian inference;Test of significance Introduction A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study (not controlled). In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold probability, the significance level. The phrase "test of significance" was coined by Ronald Fisher: "Critical tests of this kind may be called tests of significance, and when such tests are available we may discover whether a second sample is or is not significantly different from the first."[1] Hypothesis testing is sometimes called confirmatory data analysis, in contrast to exploratory data analysis. In frequency probability,these decisions are almost always made using null-hypothesis tests. These are tests that answer the question Assuming that the null hypothesis is true, what is the probability of observing a value for the test statistic that is at [] least as extreme as the value that was actually observed?) 2 More formally, they represent answers to the question, posed before undertaking an experiment,of what outcomes of the experiment would lead to rejection of the null hypothesis for a pre-specified probability of an incorrect rejection. One use of hypothesis testing is deciding whether experimental results contain enough information to cast doubt on conventional wisdom. Statistical hypothesis testing is a key technique of frequentist statistical inference. The Bayesian approach to hypothesis testing is to base rejection of the hypothesis on the posterior probability.[3][4]Other approaches to reaching a decision based on data are available via decision theory and optimal decisions. The critical region of a hypothesis test is the set of all outcomes which cause the null hypothesis to be rejected in favor of the alternative hypothesis. The critical region is usually denoted by the letter C. One-sample tests are appropriate when a sample is being compared to the population from a hypothesis. The population characteristics are known from theory or are calculated from the population.

概率论的那些事儿

概率论的那些事院系：自动化测试与控制系姓名：XXX 学号：1130110XXX 导师：XXXX

摘要：概率史是一门研究随机现象规律的数学分支。它起源于十七世纪中叶，当时在误差分析、人口统计等范筹中，有大量的随机数据资料需要整理和研究，从而孕育出一种专门研究随机现象的规律性的数学。关键字：概率论博弈发展生活发展史概率史是一门研究随机现象规律的数学分支。它起源于十七世纪中叶，当时在误差分析、人口统计等范筹中，有大量的随机数据资料需要整理和研究，从而孕育出一种专门研究随机现象的规律性的数学。另一方面，由于数学家参与讨论分赌本问题导致惠根斯完成了《论赌博中的计算》一书，由此奠定了古典概率论的基础。使概率论成为数学一个分支的另一奠基人是瑞士数学家雅各布伯努利。他的主要贡献是建立了概率论中的第一个极限定理《伯努利大数定理》。之后，法国数学家棣莫弗在他的著作《分析杂论》中提出了著名的《棣莫弗—拉普拉斯定理》。接着拉普拉斯在1812年出版了《概率的分析理论》，首先明确地对概率作了古典的定义。经过高斯和泊松等数学家的努力，概率论在数学中地位基本确立。到了20世纪的30年代，通过俄国数学家柯尔莫哥洛夫在概率论发展史上的杰出贡献，完全使概率论成为了一门严谨的数学分支。近代又出现了理论概率及应用概率论的分支，概率论被广泛的应用到了不同范筹和不同的学科。今天概率论已经成为一个非常庞大的数学分支。研究事物发生究数字重复的几率. 随着18、19世纪科学的发展，人们注意到在某些生物、物理和社会现象与机会游戏之间有某种相似性，从而由机会游戏起源的概率论被应用到这些领域中；同时这也大大推动了概率论本身的发展。使概率论成为数学的一个分支的奠基人是瑞士数学家j.伯努利，他建立了概率论中第一个极限定理，即伯努利大数定律，阐明了事件的频率稳定于它的概率。随后棣莫弗和p.s.拉普拉斯又导出了第二个基本极限定理（中心极限定理）的原始形式。拉普拉斯在系统总结前人工作的基础上写出了《分析的概率理论》，明确给出了概率的古典定义，并在概率论中引入了更有力的分析工具，将概率论推向一个新的发展阶段。19世纪末，俄国数学家p.l.切比雪夫、a.a.马尔可夫、a.m.李亚普诺夫等人用分析方法建立了大数定律及中心极限定理的一般形式，科学地解释了为什么实际中遇到的许多随机变量近似服从正态分布。20世纪初受物理学的刺激，人们开始研究随机过程。这方面a·n·柯尔莫哥洛夫、n.维纳、a·a·马尔可夫、a·r·辛钦、p·莱维及w·费勒等人作了杰出的贡献。在总体上，概率论是一门研究事情发生的可能性的学问，但是最初概率论的起源与赌博问题有关。16世纪，意大利的学者吉罗拉莫·卡尔达诺（Girolam oCardano，1501——1576）开始研究掷骰子等赌博中的一些简单问题。17世纪中叶，当时的法国宫廷贵族里盛行着掷骰子游戏，游戏规则是玩家连续掷4 次骰子，如果其中没有 6 点出现，玩家赢，如果出现一次 6 点，则庄家（相当于赌场）赢。按照这一游戏规则，从长期来看，庄家扮演赢家的角色，而玩家大部分时间是输家，因为庄家总是要靠此为生的，因此当时人们也就接受了这种现象。后来为了使游戏更刺激，游戏规则发生了些许变化，玩家这回用2 个骰子连续掷24 次，不同时出现2个6点，玩家赢，否则庄家赢。当时人们普遍认为，2 次出现 6 点的概率是一次出现 6 点的概率的 1 / 6 ，因此 6 倍于前一种规则的次数，也既是24 次赢或输的概率与以前是相等的。然而事实却刚好相反，从长期来看，这回庄家处于输家的状态，于是他们去请教当时的数

济南大学概率论A大作业答案

第一章概率论的基本概念一、填空题 1．;)3(;)2(;)1(C B A C B A C B A C B A C AB )()4(C B C A B A C B A C B A C B A C B A 或; 2． 2 1 81，； 3．6.0； 4． 733.0，； 5． 8.0,7.0； 6． 87； 7． 85； 8. 996.01211010 12或A -； 9． 2778.0185 6 446==A ；10. p -1. 二、选择题 D ；C ；B ；A ；D ； C ；D ；C ；D ；B . 三、解答题 1.解：).()()()(),((AB P B P AB P A P A B P B A P -=-∴=）相互独立，又）B A B A P B P A P ,,9 1 )(),((==∴ .3 2 )(,91)](1[)()()()(22=∴=-===∴A P A P A P B P A P B A P 2.解：设事件A 表示“取得的三个数字排成一个三位偶数”，事件B 表示“此三位偶数的末尾为0”，事件B 表示“此三位偶数的末尾不为0”，则: =)(A P )()(B P B P += .125 3 4 1 2123423=+A A A A A 3.解：设A i =“飞机被i 人击中”，i =1,2,3 , B =“飞机被击落”, 则由全概率公式： )()()()((321321B A P B A P B A P B A B A B A P B P ++== ） )()()()()()(332211A B P A P A B P A P A B P A P ++= (1) 设1H =“飞机被甲击中”，2H =“飞机被乙击中”，3H =“飞机被丙击中”, 则: =)(1A P 321(H H H P 321(H H H P 321(H H H P ) =+)(321H H H P +)(321H H H P )(321H H H P ) 由于甲、乙、丙的射击是相互独立的，

概率论

概率论与数理统计发展史

概率论大作业讲解

概率计算方法全攻略

概率论论文

概率论习题及答案()

概率统计论 浅谈泊松分布

概率论与数理统计公式整理超全免费版

概率论论文

概率论

浅谈初中教材中的概率与统计

概率论与数理统计知识点总结(免费超详细版)

概率论毕业论文外文翻译

概率论的那些事儿

济南大学概率论A大作业答案

概率统计论浅谈泊松分布